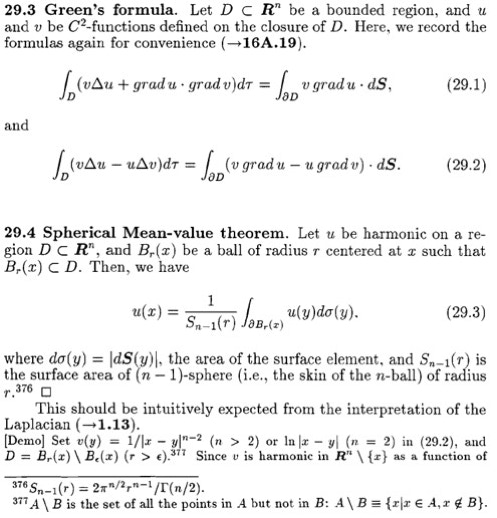Section 8. Introduction to transport phenomena

8.9

Laplacian and local averages: spherical mean-value

The conclusion in 8.9 naturally leads to a theorem called the spherical mean-value theorem for harmonic functions.

Its converse is also true: if the mean value on the sphere agrees with the value at its center for any sphere in the domain of a function u, u is a infinitely differentiable harmonic function fora a proof, see Folland,  Initroduction to partial differential equations p91). Relevant excerpts from Applicable Analysis Chapter 29 

(see https://www.dropbox.com/sh/49vzj26r0s1wain/AACiWTfCo_yOWGMFcY6kHxOY)a?dl=0 ) are attached.